Common Problem with random(min, max)

by Szymon Lipiński
tags: programming postgresql sql

There is a common problem with many homemade random functions. All languages which I know have some kind of random() function. This function returns a floating point number within the range [0.0, 1.0) with uniform distribution of values.

The random generators can have different distribution of the values, but in this entry I will just write about the uniformly distributed generator.

A uniform distribution means that each number can be returned with the same probability.

In PostgreSQL there is just the random() function. There is no function like random(min, max) which would return an integer value from the range [min, max]. Once upon a time I had to create such a function for some funny algorithm. The obvious way used on many websites to create that, is something like:

min + (max - min) * random()

… and it will return a number from the range [min, max)… sounds good.

There are just two problems with this implementation:

A Problem

Let’s check what the real problem is. A simple SQL function which you can implement in PostgreSQL, that returns such a random number is:

CREATE OR REPLACE FUNCTION
    random_range_bad(INTEGER, INTEGER)
RETURNS INTEGER AS
$$
    SELECT ($1 + ($2 - $1) * random())::INTEGER;
$$ LANGUAGE SQL;

I will also create a table for the data:

CREATE TABLE data_bad ( value INTEGER );

and I will fill that with a sample:

INSERT INTO data_bad(value)
SELECT random_range_bad(1,10)
FROM generate_series(1,10*1000*1000);

So my range is [1; 10] and there are 10M of numbers;

Let’s check the distribution.

SELECT value "VALUE", count(*) "COUNT"
FROM data_bad
GROUP BY value
ORDER BY value;

  VALUE   COUNT
  ------- -----------
   1         555,979
   2       1,111,342
   3       1,111,332
   4       1,110,525
   5       1,112,093
   6       1,110,441
   7       1,112,215
   8       1,109,548
   9       1,111,165
  10         555,360

This is not the uniform distribution. The number of every of the number should be similar. It will be the same only when we will use the random function infinite times, but that’s rather hard to implement.

What is the problem?

The main problem is the conversion to INTEGER. It works like this:

select
    (generate_series(0, 10) / 10.0)::numeric(10,1)
        "VALUE",
    (generate_series(0, 10) / 10.0)::integer
        "ROUNDED TO INTEGER";

  VALUE   ROUNDED TO INTEGER
  ------- --------------------
  0.0     0
  0.1     0
  0.2     0
  0.3     0
  0.4     0
  0.5     1
  0.6     1
  0.7     1
  0.8     1
  0.9     1
  1.0     1

The sql function returns data from the range [1, 10], but the distribution is not uniform. The value 1 is made from all numbers from the range [1.0, 1.5), while the number 2 is from the range [1.5, 2.5)… the number 10 is from the range [9.5, 10.0). The result is that we should get the values 1 and 10 less often than the rest.

The Solution

Solution is quite simple… let’s just modify the formula to something like this:

floor(min + (max - min + 1) * random)

se we take a random floating point value from the range [1, 11), and then we get the floor of that. This way the output value of 1 is taken from the range [1, 2) and so on. All of the ranges have equal length, so the distribution should be uniform (it depends on the uniform distribution of the random() function of course).

The rounding from floating point to integer for this formula looks like this:

select
    (generate_series(0, 10) / 10.0)::numeric(10,1)
        "VALUE",
    (generate_series(0, 10) / 10.0)::integer
        "ROUNDED TO INTEGER",
    floor(generate_series(0, 10) / 10.0)
        "FLOORED";

  VALUE   ROUNDED TO INTEGER   FLOORED
  ------- -------------------- ---------
  0.0     0                    0
  0.1     0                    0
  0.2     0                    0
  0.3     0                    0
  0.4     0                    0
  0.5     1                    0
  0.6     1                    0
  0.7     1                    0
  0.8     1                    0
  0.9     1                    0
  1.0     1                    0

Let’s check the generator:

CREATE TABLE data_good ( value INTEGER );
CREATE OR REPLACE FUNCTION
random_range_good(INTEGER, INTEGER) RETURNS INTEGER
AS $$
    SELECT floor(($1 + ($2 - $1 + 1) * random()))::INTEGER;
$$ LANGUAGE SQL;
INSERT INTO data_good(value)
    SELECT random_range_good(1,10)
    FROM generate_series(1,10*1000*1000);
SELECT
    value "VALUE", count(*) "COUNT"
FROM data_good
GROUP BY value
ORDER BY value;

  VALUE      COUNT
  ---------- ---------------
  1          1000532
  2          998310
  3          999804
  4          1000242
  5          999987
  6          998818
  7          1000644
  8          999577
  9          1000642
  10         1001444

The Chart

Let’s just compare the distributions:

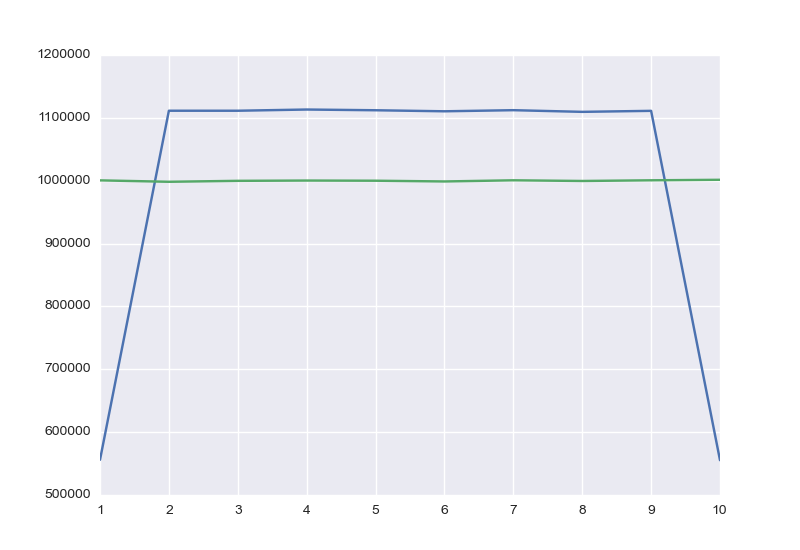
The blue line is the first function formula. The green is the second.

It looks like the distribution is OK now.

The Conclusion